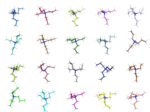This is the 3rd post in a series outlining a workflow using freely available computational chemistry resources with python interfaces […]
This is the second post in a series aiming at generating a range of candidate structures for evaluation in the […]
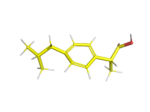
This is the first of a series examining the use of python to generate candidate structures of molecules. These conformations […]
In an effort to create a set of simple tools that are useful for data processing and realtime analysis of […]
Love it or hate it, the lack of a tractable options to create Gantt charts warrants frustration at times. A […]
Now incorporated directly into the latest version of matplotlib (v1.3) here is a great alternative that brings some style to […]